Estudo Analítico da Reta
Consideremos a reta $r$ determinada pelos pontos $A(x_A,y_A)$ e $B(x_B,y_B)$ distintos, e seja $P(x,y)$ um ponto genérico de $r$.
Como $A$, $B$ e $P$ estão alinhados, temos:
Ou Seja:
$$(y_A-y_B)\cdot x+(x_B-x_A) \cdot y +x_A\cdot y_B-x_B\cdot y_A=0$$
Fazendo $y_A-y_B=a$, $x_B-x_A=b$ e $x_A\cdot y_B-x_B\cdot y_A=c$, podemos escrever $ax+by+c=0$.
Sendo $A$ e $B$ distintos, sabemos que $x_A \neq x_B$ ou $y_A \neq y_B$, portanto, $a \neq 0$ ou $b \neq 0$, isto é, nunca ocorre $a$ e $b$ serem simultaneamente nulos.
Então, podemos afirmar:
"A toda reta do plano cartesiano podemos associar uma equação da forma $ax+by+c=0$, com $a$ e $b$ não simultaneamente nulos, sendo $x$ e $y$ as coordenadas de um ponto genérico da reta."
Do mesmo modo, a toda equação da forma $ax+by+c=0$, pode ser associada uma reta do plano cartesiano, de modo que as coordenadas de todos os seus pontos sejam soluções desta equação.
Sejam $A(x_A,y_A)$ e $B(x_B,y_B)$ dois pontos da reta e $P(x,y)$ um ponto genérico do plano cartesiano cujas coordenadas satisfaçam a equação $ax+by+c=0$.
Sendo assim, podemos escrever o sistema:
Considerando $x$, $x_A$, $x_B$, $y$, $y_A$, $y_B$ e $1$ como seus coeficientes e $a$, $b$ e $c$ como suas incógnitas, percebemos que se trata de um sistema linear homogêneo em $a$, $b$ e $c$ com soluções não-triviais. Logo:
Isso nos permite concluir que $A$, $B$ e $P$ são colineares.
A equação $ax+bx+c=0$ é chamada de equação geral ou implícita da reta.
$\alpha =0$:
Como $A$, $B$ e $P$ estão alinhados, temos:
Ou Seja:
$$(y_A-y_B)\cdot x+(x_B-x_A) \cdot y +x_A\cdot y_B-x_B\cdot y_A=0$$
Fazendo $y_A-y_B=a$, $x_B-x_A=b$ e $x_A\cdot y_B-x_B\cdot y_A=c$, podemos escrever $ax+by+c=0$.
Sendo $A$ e $B$ distintos, sabemos que $x_A \neq x_B$ ou $y_A \neq y_B$, portanto, $a \neq 0$ ou $b \neq 0$, isto é, nunca ocorre $a$ e $b$ serem simultaneamente nulos.
Então, podemos afirmar:
"A toda reta do plano cartesiano podemos associar uma equação da forma $ax+by+c=0$, com $a$ e $b$ não simultaneamente nulos, sendo $x$ e $y$ as coordenadas de um ponto genérico da reta."
Do mesmo modo, a toda equação da forma $ax+by+c=0$, pode ser associada uma reta do plano cartesiano, de modo que as coordenadas de todos os seus pontos sejam soluções desta equação.
Sejam $A(x_A,y_A)$ e $B(x_B,y_B)$ dois pontos da reta e $P(x,y)$ um ponto genérico do plano cartesiano cujas coordenadas satisfaçam a equação $ax+by+c=0$.
Sendo assim, podemos escrever o sistema:
Considerando $x$, $x_A$, $x_B$, $y$, $y_A$, $y_B$ e $1$ como seus coeficientes e $a$, $b$ e $c$ como suas incógnitas, percebemos que se trata de um sistema linear homogêneo em $a$, $b$ e $c$ com soluções não-triviais. Logo:
Isso nos permite concluir que $A$, $B$ e $P$ são colineares.
A equação $ax+bx+c=0$ é chamada de equação geral ou implícita da reta.
Inclinação e Coeficiente Angular da Reta
Consideremos uma reta $r$ qualquer e o ângulo de medida $\alpha$ que ela forma com o eixo horizontal, sendo o ângulo medido a partir do referido eixo, no sentido anti-horário.
Chamamos essa medida $\alpha$ de inclinação da reta.
Temos para $\alpha$ as seguintes possibilidades:
$\alpha =0$:
Portanto, a inclinação $\alpha$ de uma reta $r$ é tal que $0 \leq \alpha< 180$.
Por outro lado, chamamos de coeficiente angular ou declividade da uma reta $r$ não-perpendicular ao eixo $x$ o número $m$, de modo que:
$$m=\tan \alpha$$
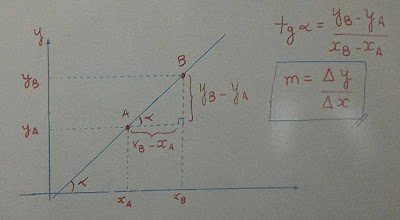
Coeficiente Angular de uma Reta dada por 2 Pontos
Consideremos os pontos $A(x_A,y_A)$ e $B(x_B,y_B)$ de uma reta $r$ não-perpendicular ao eixo $x$.
Vejamos então, os casos em que $0<\alpha <90$ e $90< \alpha <180$.
$90< \alpha <180$:
Coeficiente Linear de uma Reta
Seja uma reta $r$ de equação $ax+by+c=0$.
Quando $x=0$, a equação se reduz a $by+c=0$ ou $y=-\frac{c}{b}$, portanto o ponto onde $r$ corta o eixo vertical é:
$$(0,-\frac{c}{b})$$
O número $-\frac{c}{b}$, que indicaremos por $n$, é, então, a ordenada do ponto onde a reta $r$ corta o eixo vertical. Ele é o coeficiente linear da reta.
Equação Reduzida da Reta
Consideremos uma reta $r$ não-perpendicular ao eixo $x$ cuja equação geral é $ax+by+c=0$.
Se $A(x_A,y_A)$ e $B(x_B,y_B)$ são dois pontos distintos de $r$, podemos escrever:
Isolando $y$ no primeiro membro da equação $ax+by+c=0$, encontramos:
$$y=-\frac{a}{b}\cdot x-\frac{c}{b}$$
Como $-\frac{a}{b}=m$ e $-\frac{c}{b}=n$, então $y=mx+n$ e esta é a equação reduzida ou explícita da reta $r$.