Polinômios

Função Polinomial

A função $P: C \rightarrow C$, definida pela sentença matemática $P(x)=a_0x^n+a_1x^{n-1}+a_2x^{n-2}+\cdots + a_{n-1}x+a_n$, em que $a_0$, $a_1$, $a_2$, $\cdots$, $a_{n-1}$ e $a_n$ são números complexos com $n \in \mathbb{N}$, é chamada de função polinomial.

Os números $a_0$, $a_1$, $a_2$, $\cdots$, $a_{n-1}$ e $a_n$ são os coeficientes; as parcelas  $a_0x^n$, $a_1x^{n-1}$, $a_2x^{n-2}$, $\cdots$, $a_{n-1}x$ e $a_n$ são os termos do polinômio ou, simplesmente, monômios; $a_n$ é o termo independente e $x$ é a variável.

Valor Numérico de um Polinômio

Dado um polinômio $P(x)$, chama-se valor numérico de $P(x)$, para $x=a$, o número $P(a)$ encontrado quando substituímos $x$ por $a$ e efetuamos as operações indicadas.

Exemplo:

Raiz ou Zero de um Polinômio

Dado um polinômio $P(x)$ e um número $a$, dizemos que $a$ é raiz ou zero do polinômio $P(x)$ se, e somente se, $P(a)=0$.

Grau de um Polinômio

Seja $P(x)$ um polinômio não-nulo.

Chamamos de grau de $P(x)$ e indicamos por $gr(P)$ o maior expoente de $x$ tal que o coeficiente do termo onde esse expoente aparece seja diferente de 0.

Exemplos:

Adição, Subtração e Multiplicação

Faremos, por meio de exemplos, uma rápida revisão destas operações.

Consideremos os polinômios $P_1(x)=2x^3-5x^2+x-3$ e $P_2(x)=x^2-3x+4$.

Para somar ou subtrair polinômios, basta somar ou subtrair os coeficientes dos termos semelhantes.

Para multiplicar 2 polinômios, basta multiplicar cada termos de um deles por todos os termos do outro, e depois, reduzir os termos semelhantes.
Exemplos:

Divisão de Polinômios

A divisão de um polinômio $P(x)$, chamado de dividendo, por outro polinômio não-nulo $D(x)$, chamado de divisor, é a operação por meio da qual determinamos os polinômios $Q(x)$ e $R(x)$, chamados, respectivamente, de quociente e resto, de maneira que se verifiquem as duas condições:

$P(x)=Q(x)\cdot D(x)+R(x)$; e

$gr(R)<gr(D)$ (Quando $R(x)=0$, a divisão é chamada de exata e dizemos que $P(x)$ é divisível por $D(x)$.)

O método da chave ou algoritmo de Euclides para efetuar a divisão de polinômios será relembrado por meio do exemplo a seguir:

Calculemos, então, o quociente e o resto da divisão de $P(x)=-3x^4+6x^5+2x^2-2x+8$ por $D(x)=2x^2+1-3x$.

Inicialmente devemos verificar se os polinômios estão ordenados segundo as potências decrescentes de $x$. Ordenamos os seus termos, se necessário, e completamos o polinômio $P(x)$ caso falte algum termo.

Como $P(x)$ e $D(x)$ não estão ordenados e $P(x)$ é incompleto, devemos escrever:

Dividindo o 1° termo de $P(x)$ pelo 1° termo de $D(x)$, encontramos o 1° termo de $Q(x):

$$\frac{6x^5}{2x^2}=3x^3$$

Multiplicando $3x^3$ por $D(x)$ e subtraindo o resultado de $P(x)$, encontramos o 1° resto parcial $R_1(x)$:

Como $gr(R_1)>gr(D)$, repetimos o passo anterior, obtendo o 2° termo de $Q(x)$ e o 2° resto parcial $R_2(x)$:

Como $gr(R_2)>gr(D)$, de modo análogo achamos o 3° termo de $Q(x)$ e o 3° resto parcial $R_3(x)$:

Como $gr(R_3)<gr(D)$, da mesma maneira obtemos o 4° termo de $Q(x)$ e o 4° resto parcial $R_4(x)$:

Como $gr(R_4)>gr(D)$, o processo está acabado. Temos $Q(x)=3x^3+3x^2+3x+4$ e $R(x)=7x+4$.

Dispositivo Prático de Briot-Ruffini

Quando queremos dividir um polinômio $P(x)$ por $x-a$ podemos nos valer de um algoritmo chamado Dispositivo Prático de Briot-Ruffini, no qual trabalhamos somente com os coeficientes de $P(x)$ e com a raiz de $x-a$.

Consideremos, como exemplo, a divisão de $P(x)=x^4-5x^3+x^2-3x+6$ por $x-2$.

Em primeiro lugar, devemos dispor os coeficientes de $P(x)$ e a raiz de $x-2$, conforme o esquema abaixo:

O 1° passo é "abaixar" o 1° coeficiente de $P(x)$ que, neste exemplo, é 1:

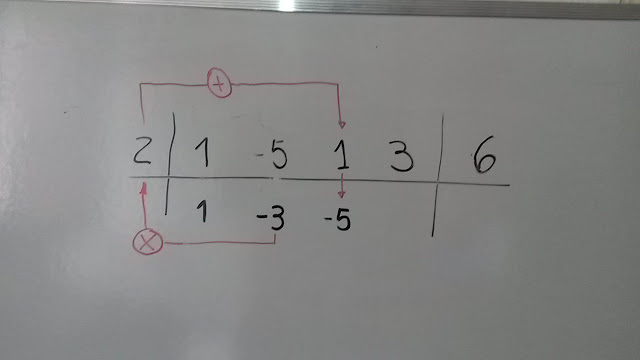
Em seguida, multiplica-se 1 por 2 e soma-se o produto obtido com o 2° coeficiente de $P(x)$. O resultado encontrado, $1 \cdot 2+(-5)=-3$, é o 2° coeficiente do quociente procurado.

O passo seguinte é multiplicar $-3$ por 2 e somar o produto obtido com o 3° coeficiente de $P(x)$. O novo resultado encontrado, $-3 \cdot 2+1=-5$, é o 3° coeficiente do quociente.

Em seguida, de modo análogo, multiplica-se $-5$ por $2$ e soma-se com o 4° coeficiente de $P(x)$. O resultado encontrado, $-5 \cdot 2+(-3)=-13$, é o 4° coeficiente do quociente.

Para finalizar, repete-se o processo para o número $-13$, obtendo-se $-20$ $(-13 \cdot 2+6)=-20$, que é o resto da divisão.

O quociente procurado é $Q(x)=x^3-3x^2-5x-13$ e o resto é $R=-20$.