Demonstrações
Para um real entendimento sobre determinado tema, mais importante do que decorar certas fórmulas é entender o raciocínio utilizado para se chegar a essa expressão. Venho por meio dessa série de post's, demonstrar algumas fórmulas usadas na Matemática e Física.
-------------------------------------------------------------------------------------------------------------------Demonstração do Teorema de Pitágoras
O Teorema de Pitágoras pode ser escrito da seguinte forma:
"Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos."
Ou seja, em um triângulo ABC com hipotenusa em "$a$" e catetos nos lados "$b$" e "$c$", temos que:
$$a^2=b^2+c^2$$
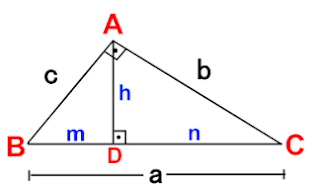
Começaremos imaginando uma reta que irá sair do vértice A, perpendicularmente em direção a "$a$" e diremos que o ponto de encontro se chamará "$D$". Assim temos:
Note que essa reta representa a altura do triângulo. Chamaremos ela de $h$. Note também que o lado "$a$" ficou dividido em 2 partes, aqui chamados de "$m$" e "$n$". Ficamos com a seguinte situação:
Dizendo que os vértices B e C formam ângulos "$x$" e "$y$" respectivamente, temos:
Tendo em vista que a soma dos ângulos internos de um triângulo é 180°, podemos esquematizar:
Essa figura nos permite dizer que os triângulos são semelhantes, logo, separando a figura em 3 triângulos temos:
Olhando para os triângulos ABC e ABD, temos:
$$\frac{AB}{BD}=\frac{BC}{AB} \therefore \frac{c}{m}=\frac{a}{c}$$
$$c^2=am$$
Olhando para os triângulos ABC e ADC, temos:
$$\frac{AC}{CD}=\frac{BC}{AC} \therefore \frac{b}{n}=\frac{a}{b}$$
$$b^2=an$$
Somando-se essas duas expressões, temos:
$$b^2+c^2=an+am$$
Evidenciando "$a$":
$$b^2+c^2=a(n+m)$$
Sugiro que voltem à 3° imagem, e reparem que o lado "$a$" foi dividido em 2 partes "$m$" e "$n$", portanto:
$$n+m=a$$
Agora, substituindo ficamos:
$$b^2+c^2=a \cdot a \therefore a^2=b^2+c^2$$