Introdução
O termo hidrostática se refere ao estudo dos fluidos em repouso. Um fluido é uma substância que pode escoar facilmente e que muda de forma sob a ação de pequenas forças. Portanto o termo fluido inclui os líquidos e gases.
Para desenvolvermos o estudo da hidrostática, é indispensável o conhecimento de duas grandezas: A pressão e a massa específica. Portanto iniciaremos essa postagem analisando esses conceitos.
Para desenvolvermos o estudo da hidrostática, é indispensável o conhecimento de duas grandezas: A pressão e a massa específica. Portanto iniciaremos essa postagem analisando esses conceitos.
Pressão e Massa Específica
Consideremos um objeto, cujo peso iremos denominar $\vec{F}$, apoiado sobre uma superfície plana, como mostra a figura abaixo:
Seja $A$ a área na qual o objeto se apóia. Observe que a compressão que o objeto exerce sobre a superfície, devido ao seu peso, está distribuída em toda a área $A$ e a força $\vec{F}$, que produz a compressão, é perpendicular à superfície, e distribuída sobre a área $A$, da seguinte maneira:
$$p=\frac{F}{A}$$
A relação entre as unidades de pressão pode ser vista a seguir:
Seja $A$ a área na qual o objeto se apóia. Observe que a compressão que o objeto exerce sobre a superfície, devido ao seu peso, está distribuída em toda a área $A$ e a força $\vec{F}$, que produz a compressão, é perpendicular à superfície, e distribuída sobre a área $A$, da seguinte maneira:
$$p=\frac{F}{A}$$
A relação entre as unidades de pressão pode ser vista a seguir:
Já a massa específica, ou densidade absoluta de um corpo será representada pela letra grega rô e definida da seguinte maneira:
$$\rho=\frac{m}{V}$$
$$\rho=\frac{m}{V}$$
No SI, a unidade utilizada é o kg/m³, porém é muito usual a utilização da unidade g/cm³.
Para transformar de g/cm³ para kg/m³, basta multiplicar por 1000.
A Pressão Atmosférica
O ar, como qualquer substância próxima à Terra, é atraído por ela, isto é, tem peso.
Em virtude disto, a camada atmosférica que envolve a Terra, atingindo uma altura de dezenas de quilômetros, exerce uma pressão sobre os corpos nela mergulhados. Essa pressão recebe o nome de pressão atmosférica.
Afim de determinar seu valor, Torricelli tomou um tubo de vidro, com cerca de 1m de comprimento, fechado em uma das pontas, enchendo-o completamente com mercúrio.
Tapando a extremidade livre e invertendo o tubo, mergulhou essa extremidade em um recipiente contendo também mercúrio. Ao destampar o tubo, verificou que a coluna líquida descia, até estacionar a uma altura de cerca de $76cm$ acima do nível de mercúrio no recipiente. Concluiu, então, que a pressão atmosférica, $P_a$, atuando sobre a superfície do líquido no recipiente, conseguia equilibrar a coluna de mercúrio.
Observe que, acima do mercúrio, no tubo, temos vácuo, pois, se fosse feito um orifício no tubo nessa região de modo a permitir a entrada de ar, a coluna desceria até se nivelar com o mercúrio do recipiente.
Como a altura da coluna líquida no tubo era de $76cm$. Torricelli chegou à conclusão de que o valor da pressão atmosférica equivale à $76cm$ de $Hg$.
Em virtude disto, a camada atmosférica que envolve a Terra, atingindo uma altura de dezenas de quilômetros, exerce uma pressão sobre os corpos nela mergulhados. Essa pressão recebe o nome de pressão atmosférica.
Afim de determinar seu valor, Torricelli tomou um tubo de vidro, com cerca de 1m de comprimento, fechado em uma das pontas, enchendo-o completamente com mercúrio.
Tapando a extremidade livre e invertendo o tubo, mergulhou essa extremidade em um recipiente contendo também mercúrio. Ao destampar o tubo, verificou que a coluna líquida descia, até estacionar a uma altura de cerca de $76cm$ acima do nível de mercúrio no recipiente. Concluiu, então, que a pressão atmosférica, $P_a$, atuando sobre a superfície do líquido no recipiente, conseguia equilibrar a coluna de mercúrio.
Observe que, acima do mercúrio, no tubo, temos vácuo, pois, se fosse feito um orifício no tubo nessa região de modo a permitir a entrada de ar, a coluna desceria até se nivelar com o mercúrio do recipiente.
Como a altura da coluna líquida no tubo era de $76cm$. Torricelli chegou à conclusão de que o valor da pressão atmosférica equivale à $76cm$ de $Hg$.
Variação da Pressão com a Profundidade
Já sabemos que a pressão atmosférica diminui à medida que nos elevamos na atmosfera. Naturalmente, isto deveria ocorrer, pois o peso da camada de ar, que exerce a pressão atmosférica em um dado local, é tanto menor quanto maior for a altitude do local.
Quando mergulhamos em uma piscina, observamos uma situação semelhante. À medida que nos aprofundamos na água, a pressão aumenta, pois o peso da camada líquida que exerce a pressão em um ponto, é tanto maior quanto maior for a profundidade deste ponto.
Este fato ocorre em todos os fluidos, de um modo geral. A seguir, vamos estabelecer uma relação matemática que nos permitirá calcular a pressão no interior de um fluido, em uma dada profundidade.
A dedução da fórmula da pressão hidrostática pode ser visualizada aqui.
Já a pressão total que é exercida sobre um ponto é dado por:
$$P_T=P_a+P_H$$
Pela equação $P_T=P_a+P_H$, vemos que, se $h=0$, temos $P_T=P_a$ (estamos na superfície do líquido) e, à medida que $h$ aumenta, a pressão aumenta linearmente com $h$. Então, o gráfico Pxh, para um dado líquido, terá o aspecto mostrado a seguir:
Quando mergulhamos em uma piscina, observamos uma situação semelhante. À medida que nos aprofundamos na água, a pressão aumenta, pois o peso da camada líquida que exerce a pressão em um ponto, é tanto maior quanto maior for a profundidade deste ponto.
Este fato ocorre em todos os fluidos, de um modo geral. A seguir, vamos estabelecer uma relação matemática que nos permitirá calcular a pressão no interior de um fluido, em uma dada profundidade.
A dedução da fórmula da pressão hidrostática pode ser visualizada aqui.
Já a pressão total que é exercida sobre um ponto é dado por:
$$P_T=P_a+P_H$$
Pela equação $P_T=P_a+P_H$, vemos que, se $h=0$, temos $P_T=P_a$ (estamos na superfície do líquido) e, à medida que $h$ aumenta, a pressão aumenta linearmente com $h$. Então, o gráfico Pxh, para um dado líquido, terá o aspecto mostrado a seguir:
Vasos Comunicantes
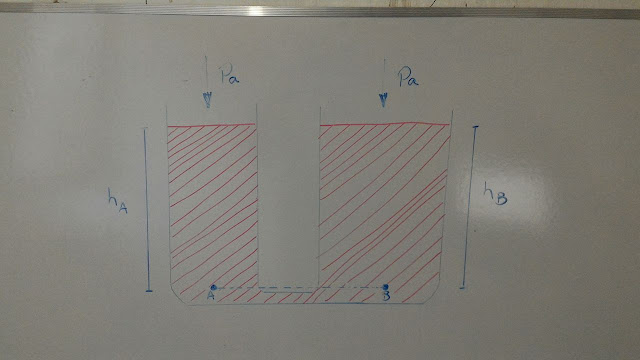
Consideremos, a seguir, dois recipientes, que não precisam ser iguais, cujas bases estão ligadas por meio de um tubo:
Dizemos que os recipientes são vasos comunicantes. Coloquemos um líquido qualquer nestes vasos e esperemos que seja atingida a situação de equilíbrio. Os pontos $A$ e $B$, situados em um mesmo nível horizontal, devem estar submetidos a pressões iguais, pois, do contrário, o líquido não estaria em equilíbrio.
Sendo $\rho$ a densidade do líquido, podemos escrever:
$$P_A=P_a+\rho\cdot g \cdot h_A$$
$$P_B=P_a+ \rho \cdot g \cdot h_B$$
Como $P_A=P_B$, concluímos que $h_A=h_B$, isto é, em vasos comunicantes, um dado líquido atinge alturas iguais em ambos os recipientes. Esta conclusão é válida mesmo que tenhamos vários recipientes que se comunicam, independentemente de suas formas ou tamanhos, conforme você pode verificar experimentalmente:
Princípio de Pascal
Consideremos um líquido, em equilíbrio, no interior de um recipiente, como está mostrado a seguir:
Nos pontos 1 e 2, as pressões valem $P_1$ e $P_2$, respectivamente. Se, por um processo qualquer, aumentarmos de $\Delta P_1$ a pressão em 1, a pressão em 2 sofrerá um aumento de pressão $\Delta P_2$. Pela relação $P_2=P_1+\rho\cdot g \cdot h$, podemos facilmente perceber que:
$$\Delta P_1=\Delta P_2$$
Isto é, o aumento de pressão em um ponto 2 é igual ao aumento da pressão provocado no ponto 1. Este fato foi descoberto por Pascal, que assim o enunciou: "O aumento da pressão, em um ponto de um líquido em equilíbrio, transmite-se integralmente a todos os pontos deste líquido". Em virtude disto, esta propriedade dos líquidos é denominada Princípio de Pascal.
Empuxo
Quando mergulhamos um corpo qualquer em um líquido, verificamos que este exerce, sobre o corpo, uma força de sustentação, isto é, uma força dirigida para cima, que tende a impedir que o corpo afunde no líquido.
Essa força é vertical, dirigida para cima, e se denomina empuxo do líquido sobre o corpo mergulhado.
Segundo Arquimedes, o empuxo que atua em um corpo mergulhado em um líquido é igual ao peso do líquido deslocado pelo corpo.
Há 3 possibilidades:
Segundo Arquimedes, o empuxo que atua em um corpo mergulhado em um líquido é igual ao peso do líquido deslocado pelo corpo.
Há 3 possibilidades:
Empuxo e Densidade do Líquido
Pelo Princípio de Arquimedes, sabemos que o empuxo é igual ao peso do líquido deslocado, ou:
$$E=m_d\cdot g$$
Onde $m_d$ é a massa do líquido deslocado.
Sendo $\rho_L$ a densidade do líquido e $V_d$ o volume deslocado, temos:
$$m_d=\rho_L\cdot V_d \rightarrow E=\rho_L\cdot V_d\cdot g$$
Por outro lado, o peso $P$ do corpo mergulhado pode ser expresso em função de sua densidade, e do seu volume, da seguinte maneira:
$$P=\rho \cdot V\cdot g$$