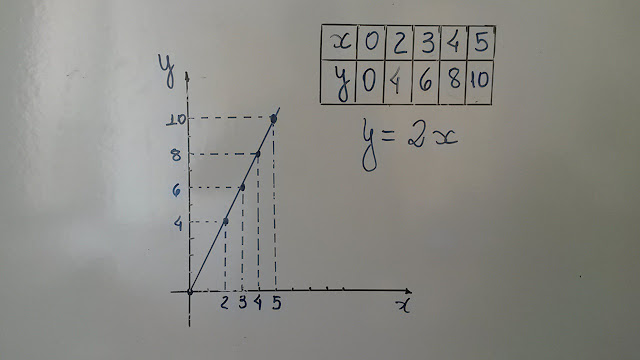Funções

Funções

Sempre que temos dois conjuntos e algum tipo de regra ou lei de formação, por meio da qual a todo elemento do primeiro conjunto corresponda a um único elemento do segundo, existe uma função.

Consideremos os conjuntos $A=\{1,2,3,4,5\}$ e $B=\{6,7,8,9,10,11,12\}$. Escolhendo as letras $x$ e $y$ para representar os elementos de $A$ e $B$, respectivamente, temos que:

$x$ pode receber os valores $1,2,3,4,5$;

$y$ pode receber os valores $6,7,8,9,10,11,12$.

Seja $y=x+5$ a lei de formação.
Substituindo-se os valores que $x$ pode assumir na equação dada  efetuando os cálculos, obtemos os correspondentes valores de $y$:
$$x=1 \rightarrow y=1+5=6 \rightarrow y=6$$

$$x=2 \rightarrow y=2+5=7 \rightarrow y=7$$

$$x=3 \rightarrow y=3+5=8 \rightarrow y=8$$

$$x=4 \rightarrow y=4+5=9 \rightarrow y=9$$

$$x=5 \rightarrow y=5+5=10 \rightarrow y=10$$

A função acima pode ser representada por um diagrama de flechas, modo esquemático bastante simples e muito utilizado, que indica os pares de valores $x$ e $y$ que se correspondem:

Dizemos que:

$6,7,8,9,10$ são imagens de $1,2,3,4,5$ respectivamente;

$11,12$ não são imagens de elementos de $A$, pois não são correspondentes de nenhum valor de $x$.

Temos ainda:

O conjunto imagem da função, indicado por $I_m$, é o conjunto de todas as imagens. Assim: $I_m=\{6,7,8,9,10\}$;

O conjunto $A$ é chamado de domínio da função e costuma ser indicado por $D$;

O conjunto $B$ é chamado de contra-domínio da função e costuma ser indicado por $CD$;

Quando representamos uma função qualquer com diagrama de flechas, duas condições devem ser verificadas:
1) Todo elemento de $A$ é ponto de partida de uma flecha;

2) De cada elemento de $A$ deve partir uma única flecha. 

Zeros de uma Função

Dada uma função $y=f(x)$, os valores de $x$ para os quais $f(x)=0$ são chamados zeros ou raízes da função.

No gráfico cartesiano da função, os zeros são as abscissas dos pontos onde o gráfico corta o eixo horizontal.

Exemplo: Calcule os zeros da função $f(x)=x^2-4$:
$$x^2-4=0 \therefore x^2=4 \rightarrow x=\pm \sqrt{4}=\pm 2$$

Função Constante

Chamamos de função constante toda função $f:A \rightarrow B$,$A\subset \mathbb{R}$ e $B \subset \mathbb{R}$, definida por $f(x)=c$, na qual $c$ é uma constante.

O conjunto imagem dessa função é, portanto, $I_m=\{c\}$ e o diagrama de flechas é do tipo:

Como na função constante todos os elementos do domínio têm a mesma imagem, o diagrama cartesiano é formado por pontos que têm a mesma ordenada.

Função Polinomial do 1º Grau

Toda função $f:\mathbb{R} \rightarrow \mathbb{R}$ definida por $f(x)=ax+b$, com $a \in \mathbb{R}^{*}$ e $b \in \mathbb{R}$, é chamada função polinomial do 1° grau ou função afim.

A representação da função do 1° grau é sempre uma reta inclinada em relação ao eixo horizontal. Essa inclinação depende do sinal de $a$, na função $y=ax+b$. Temos, então, 2 situações:

Função Linear

A função linear é definida como $f(x)=ax$ e seu gráfico corta o eixo vertical no ponto $(0,0)$, ou seja, passa pela origem.

Exemplo: $f(x)=2x$:

Sistemas de Inequações do 1° Grau

Um sistema de inequações é constituído de duas ou mais inequações que devem ser satisfeitas simultaneamente. Os valores encontrados formam o conjunto solução do sistema, que é o conjunto intersecção dos conjuntos soluções das inequações que compõe o sistema.

Exemplo:

Inequação-Produto

Há certos tipos de inequações nas quais aparecem produtos de termos do tipo $ax+b$, cujas resoluções dependem do estudo da variação do sinal da função polinomial do 1° grau. São as chamadas inequações-produto.

Exemplo:

Inequação-Quociente

Outra aplicação do estudo da variação de sinal da função polinomial do 1° grau é na resolução de inequações em que encontramos quocientes envolvendo termos do tipo $ax+b$. São as chamadas inequações-quociente.

Exemplos:

Função do 2° Grau

Toda função $f: \mathbb{R} \rightarrow \mathbb{R}$ definida por $f(x)=ax^2+bx+c$, com $a \in \mathbb{R}^{*}$ e $b,c \in \mathbb{R}$, é chamada de função polinomial do 2° grau.

O domínio e o contradomínio dessa função são o conjunto $\mathbb{R}$.

Zeros da Função do 2° Grau

Os zeros da função do 2° grau são os valores para os quais $f(x)=0$.
Para obtê-los, basta aplicar a fórmula resolvente do 2° grau:
$$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$$

Podem ocorrer 3 situações distintas em relação ao $\Delta$ ($b^2-4ac$):

$\Delta>0 \rightarrow$ $f(x)$ tem 2 zeros reais e diferentes;

$\Delta=0 \rightarrow$ $f(x)$ tem 2 zeros reais e iguais;

$\Delta<0 \rightarrow$ $f(x)$ não tem zeros reais.

O gráfico da função do 2° grau pode obter as seguintes formas:

Coordenadas do Vértice

A demonstração das coordenadas do vértice já foi postada aqui no blog. Ainda não viu? Não deixe de conferir!
Post - Demonstração do Vértice da Parábola

Função Exponencial

A seguinte tabela lista as propriedades de potenciação:

De acordo com $P2$ implica que:
$$a^0=1$$

Temos também, de acordo com $P2$:

$$a^{-n}=\frac{1}{a^n}$$

A tabela a seguir lista as propriedades de radiciação:

Lembrando que podemos escrever qualquer raiz na forma exponencial da seguinte maneira:
$$\sqrt[q]{a^p}=a^{\frac{p}{q}}$$

Outra propriedade importante antes de iniciarmos com Função exponencial é:
$$a^m=a^n \rightarrow m=n$$

A função $f:\mathbb{R}\rightarrow \mathbb{R}^{*}_+$, definida por $f(x)=a^x$, com $a \in \mathbb{R}^{*}_+$ e $a\neq 1$, é chamada de função exponencial de base $a$.

O gráfico da função exponencial pode assumir as seguintes formas: